Z3

发表于 更新于 Valine： 本文字数： 4.1k 阅读时长 ≈ 4 分钟

Z3学习

先来看官方文档

https://ericpony.github.io/z3py-tutorial/guide-examples.htm

这个博客也不错

https://blog.csdn.net/qq_38154820/article/details/108656598

基本使用

基本语句

Op Mnmonics Description
0 true 恒真
1 flase 恒假
2 = 相等
3 distinct 不同
4 ite if-then-else
5 and n元 合取（其中条件必须全部满足）
6 or n元 析取（其中条件满足之一即可）
7 iff implication
8 xor 异或
9 not 否定
10 implies Bi-implications

1、创建容器

s=Solver()

2、创建变量，变量有Int(整型)、BitVector(字节)、数组

3、添加约束条件

s.add(约束条件)，需要注意Int不能进行移位运算，python除是//

4、判断是否存在

1
2
3
4
5
if s.check() == sat:  
    m = s.model()  
    print(m)
else:  
    print("no answer")

变量为整型

题目

https://buuoj.cn/challenges#[ACTF新生赛2020]Universe_final_answer

关键代码

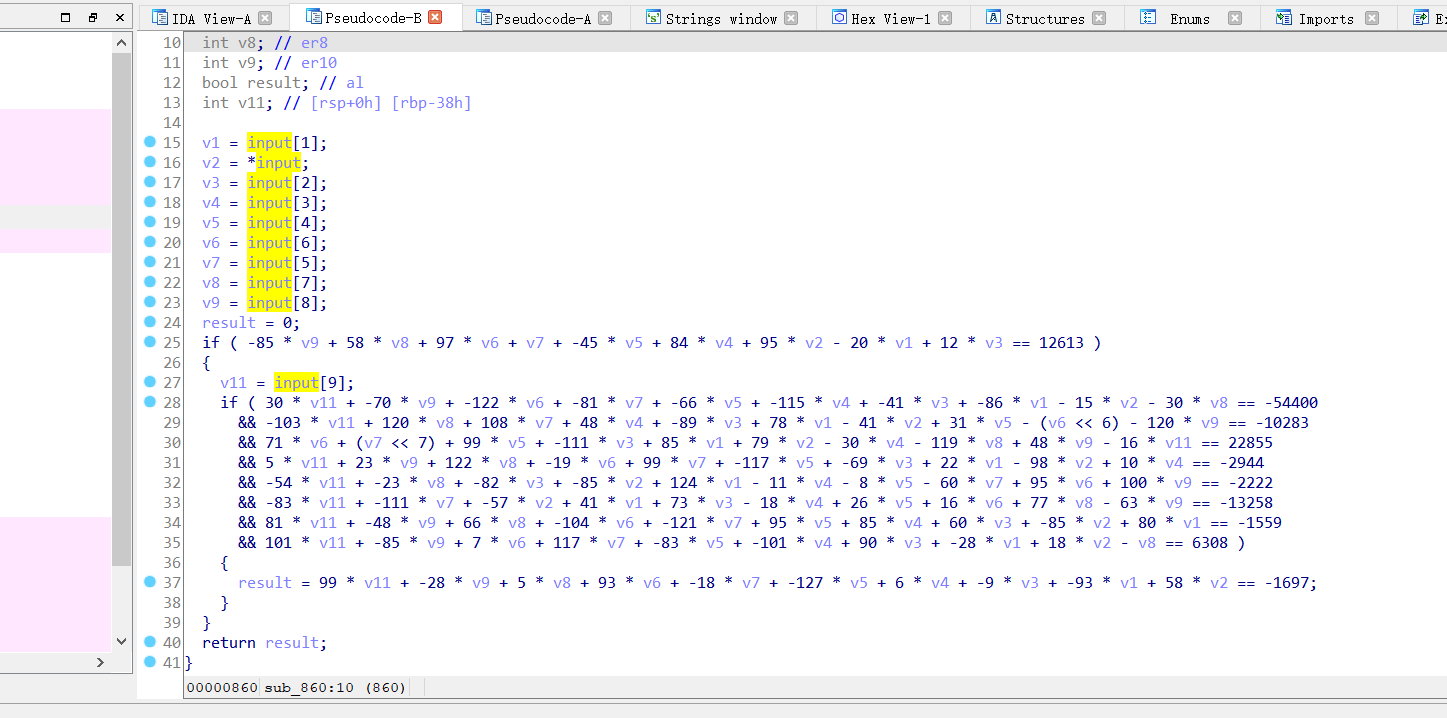
这里就直接放脚本了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from z3 import*

s=Solver()
v1=Int('v1')
v2=Int('v2')
v3=Int('v3')
v4=Int('v4')
v5=Int('v5')
v6=Int('v6')
v7=Int('v7')
v8=Int('v8')
v9=Int('v9')
v11=Int('v11')

s.add(-85 * v9 + 58 * v8 + 97 * v6 + v7 + -45 * v5 + 84 * v4 + 95 * v2 - 20 * v1 + 12 * v3 == 12613)
s.add(-85 * v9 + 58 * v8 + 97 * v6 + v7 + -45 * v5 + 84 * v4 + 95 * v2 - 20 * v1 + 12 * v3 == 12613)
s.add(-103 * v11 + 120 * v8 + 108 * v7 + 48 * v4 + -89 * v3 + 78 * v1 - 41 * v2 + 31 * v5 - (v6 *64) - 120 * v9 == -10283)
s.add(71 * v6 + (v7 *128) + 99 * v5 + -111 * v3 + 85 * v1 + 79 * v2 - 30 * v4 - 119 * v8 + 48 * v9 - 16 * v11 == 22855)
s.add(5 * v11 + 23 * v9 + 122 * v8 + -19 * v6 + 99 * v7 + -117 * v5 + -69 * v3 + 22 * v1 - 98 * v2 + 10 * v4 == -2944)
s.add(-54 * v11 + -23 * v8 + -82 * v3 + -85 * v2 + 124 * v1 - 11 * v4 - 8 * v5 - 60 * v7 + 95 * v6 + 100 * v9 == -2222)
s.add(-83 * v11 + -111 * v7 + -57 * v2 + 41 * v1 + 73 * v3 - 18 * v4 + 26 * v5 + 16 * v6 + 77 * v8 - 63 * v9 == -13258)
s.add(81 * v11 + -48 * v9 + 66 * v8 + -104 * v6 + -121 * v7 + 95 * v5 + 85 * v4 + 60 * v3 + -85 * v2 + 80 * v1 == -1559)
s.add(101 * v11 + -85 * v9 + 7 * v6 + 117 * v7 + -83 * v5 + -101 * v4 + 90 * v3 + -28 * v1 + 18 * v2 - v8 == 6308)
s.add(99 * v11 + -28 * v9 + 5 * v8 + 93 * v6 + -18 * v7 + -127 * v5 + 6 * v4 + -9 * v3 + -93 * v1 + 58 * v2 == -1697)

if s.check()==sat:
    result=s.model()

print(result)

变量为数组

题目

https://buuoj.cn/challenges#[GWCTF 2019]xxor

关键代码

1
2
3
4
5
6
7
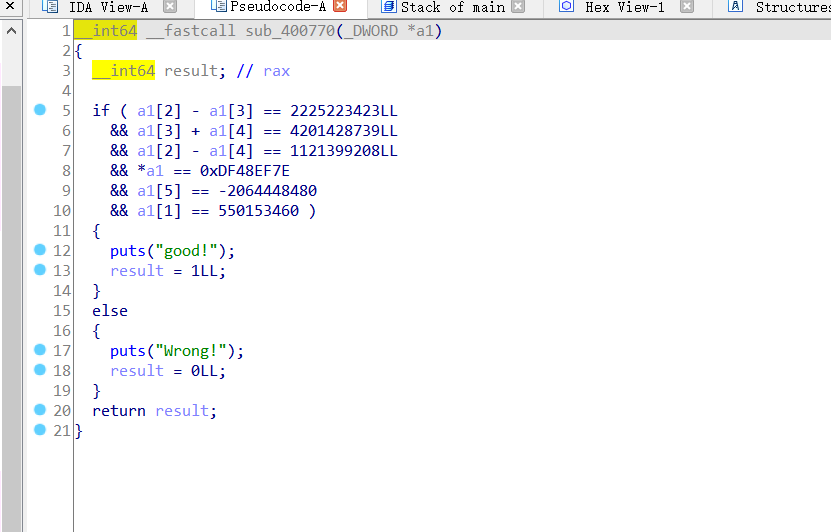
8
from z3 import*
#添加六个Int数据到s变量中
s = [Int('s%d' % i) for i in range(6)]
a=Solver()
#多个约束条件可以使用逗号间隔
a.add(s[2]-s[3]==2225223423,s[3]+s[4]==4201428739,s[2]-s[4]==1121399208,s[0]==0xdf48ef7e,s[5]==0x84f30420,s[1]==0x20caacf4)
if a.check() == sat:
    print(a.model())

这样得到的结果不会是数组的形式，如下得到的是数组形式

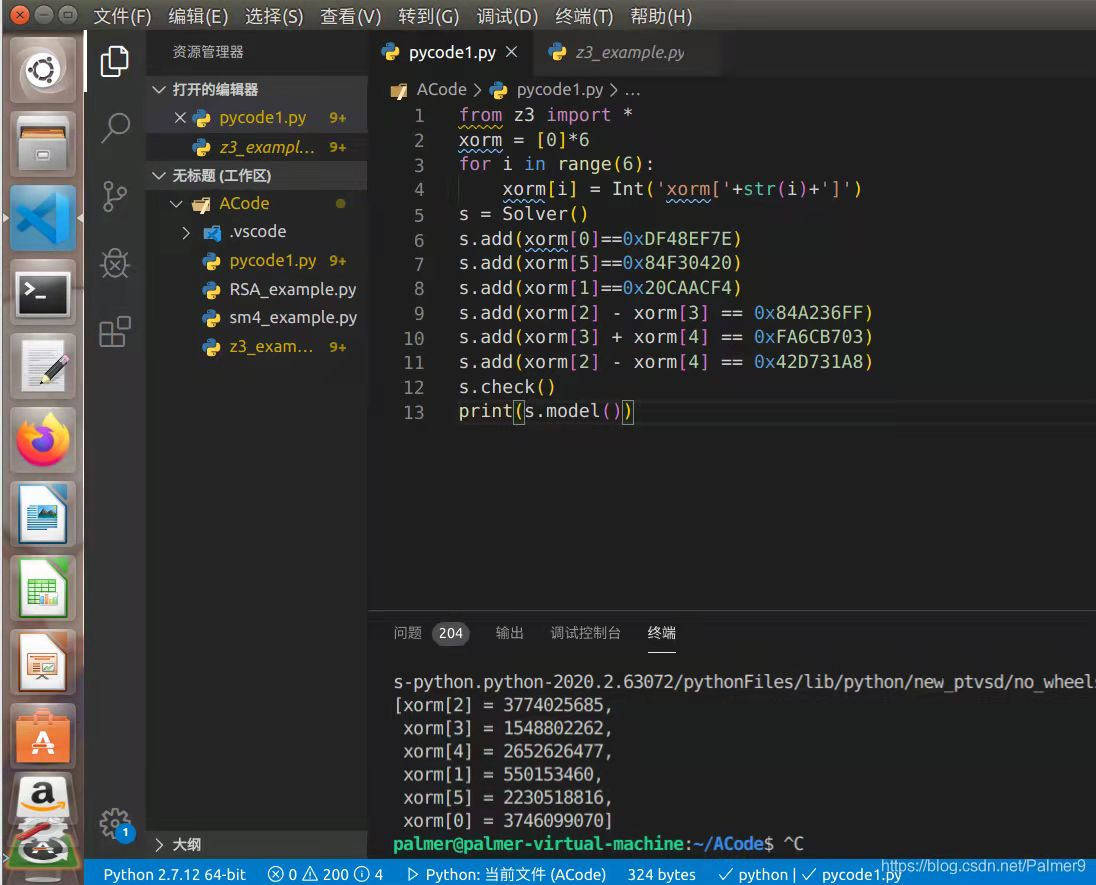
数独问题

数独问题就是9×9的方块填数（只能是1-9），分成3×3的小方块，行列数字不同，每个小方块数字不能重复

先贴一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from z3 import *
# 9x9整数变量矩阵
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(9) ]
      for i in range(9) ]
 
 
# 每个单元格包含{1，…，9}中的值
cells_c  = [ And(1 <= X[i][j], X[i][j] <= 9)
             for i in range(9) for j in range(9) ]
 
 
# 每行最多包含一个数字一次
rows_c   = [ Distinct(X[i]) for i in range(9) ]
 
 
# 每列最多包含一个数字
cols_c   = [ Distinct([ X[i][j] for i in range(9) ])
             for j in range(9) ]
 
 
# 每个3x3正方形最多包含一个数字
sq_c     = [ Distinct([ X[3*i0 + i][3*j0 + j]
                        for i in range(3) for j in range(3) ])
             for i0 in range(3) for j0 in range(3) ]
 
 
sudoku_c = cells_c + rows_c + cols_c + sq_c
 
 
# 数独实例，我们用'0'表示空单元格
instance = ((0,0,0,0,9,4,0,3,0),
            (0,0,0,5,1,0,0,0,7),
            (0,8,9,0,0,0,0,4,0),
            (0,0,0,0,0,0,2,0,8),
            (0,6,0,2,0,1,0,5,0),
            (1,0,2,0,0,0,0,0,0),
            (0,7,0,0,0,0,5,2,0),
            (9,0,0,0,6,5,0,0,0),
            (0,4,0,9,7,0,0,0,0))
 
 
instance_c = [ If(instance[i][j] == 0,
                  True,
                  X[i][j] == instance[i][j])
               for i in range(9) for j in range(9) ]
 
 
s = Solver()
s.add(sudoku_c + instance_c)
if s.check() == sat:
    m = s.model()
    r = [ [ m.evaluate(X[i][j]) for j in range(9) ]
          for i in range(9) ]
    print_matrix(r)
else:
    print("failed to solve")

题目

这是改了的数独，比较简单，拿来练练手

https://buuoj.cn/challenges#[GUET-CTF2019]number_game

Z3在题目的运用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from z3 import *

# 5*5整数变量矩阵
X = [[Int("x_%s_%s" % (i + 1, j + 1)) for j in range(5)]
     for i in range(5)]

# 每个单元格包含{0，…，4}中的值
cells_c = [And(0 <= X[i][j], X[i][j] <= 4)
           for i in range(5) for j in range(5)]

# 每行最多包含一个数字一次
rows_c = [Distinct(X[i]) for i in range(5)]

# 每列最多包含一个数字
cols_c = [Distinct([X[i][j] for i in range(5)])
          for j in range(5)]

# 每个5x5正方形最多包含一个数字,i0和j0表示分为几组
sq_c = [Distinct([X[5 * i0 + i][5 * j0 + j]
                  for i in range(5) for j in range(5)])
        for i0 in range(0) for j0 in range(0)]

sudoku_c = cells_c + rows_c + cols_c + sq_c

# 数独实例，我们用'5'表示空单元格
instance = ((1,4,5,2,3),(3,0,5,1,5),(0,5,2,3,5),(5,3,5,5,5),(4,2,5,5,1))

instance_c = [If(instance[i][j] == 5,
                 True,
                 X[i][j] == instance[i][j])
              for i in range(5) for j in range(5)]

s = Solver()
s.add(sudoku_c + instance_c)
if s.check() == sat:
    m = s.model()
    r = [[m.evaluate(X[i][j]) for j in range(5)]
         for i in range(5)]
    print_matrix(r)
else:
    print("failed to solve")