AES
¶简单介绍
AES属于分组加密算法,即加解密都是使用同一密钥,但是是分为几组进行加密
明文长度固定为128位的倍数
密钥长度可以是128、192、256位
¶加密流程
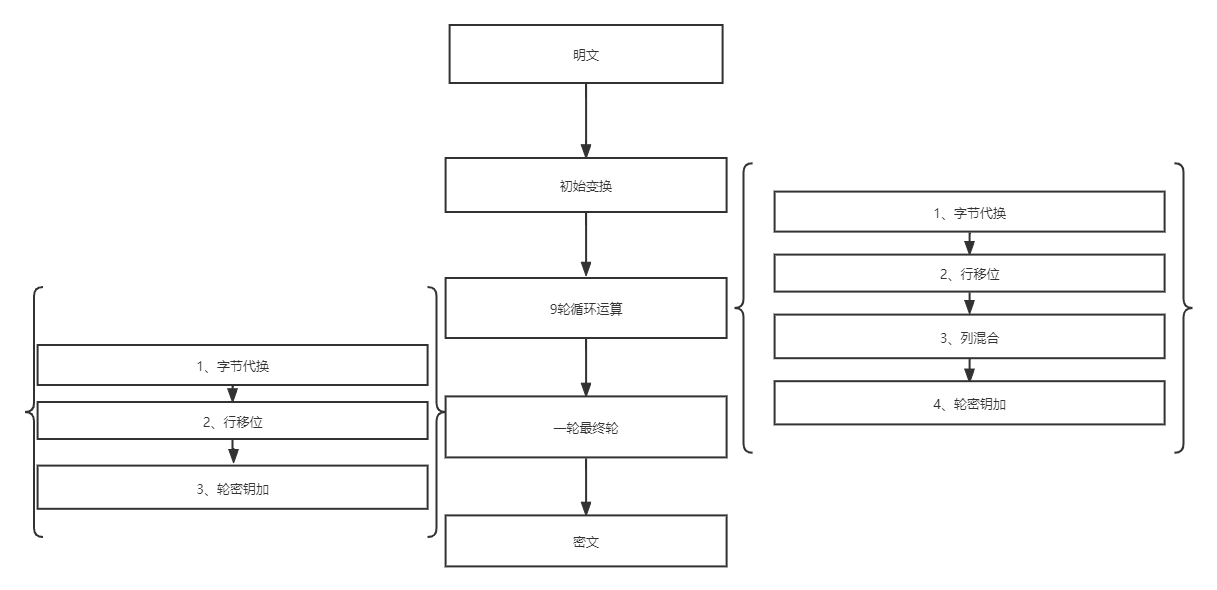
¶初始变换
这里以16字节为例子
明文放入矩阵中

子密钥放入矩阵,这里有省略号是因为后面会根据子密钥进行密钥扩展,初始变换取得是密钥扩展后的第0轮密钥

明文矩阵和子密钥矩阵进行异或-轮密钥加
对应位置进行逐字节异或

¶字节代换
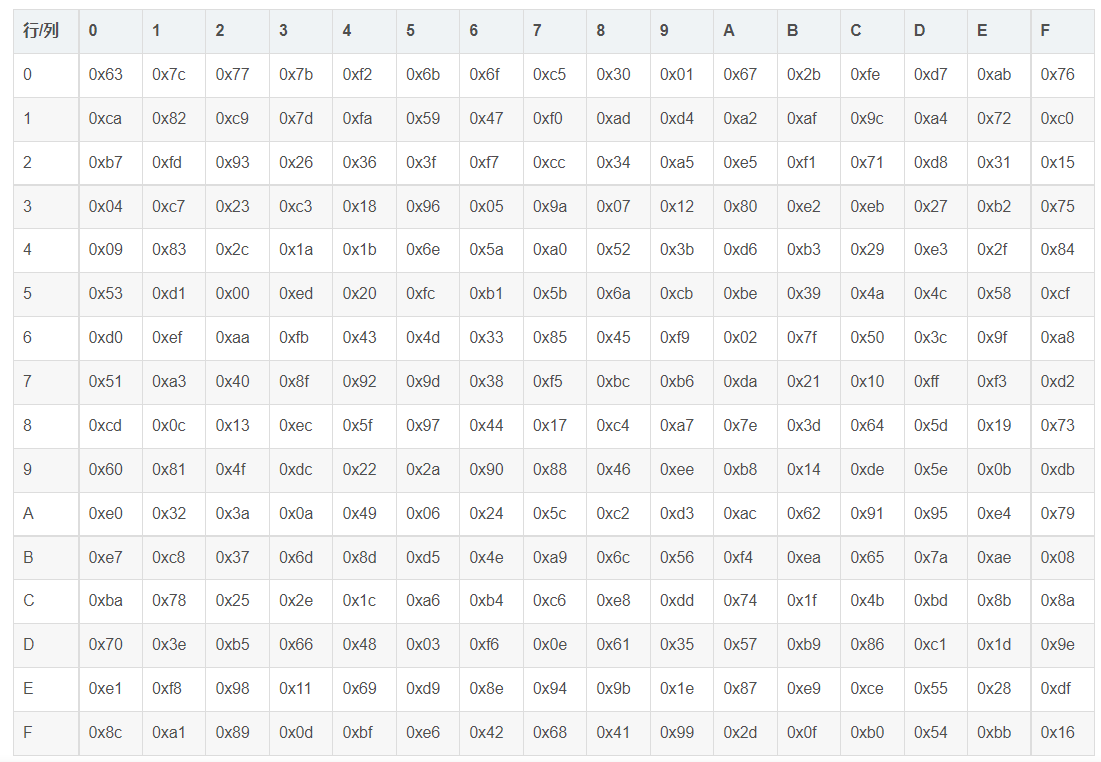
AES算法会生成一个Sbox盒用于字节代换
代换方法:假如某个字节是D4,那么找到D4的位置,xy坐标结合就是代换后的结果,这里为19
¶行移位

¶列混合
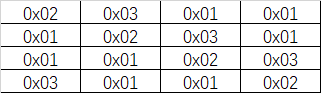
将输入的4×4矩阵左乘一个给定的4×4矩阵
这里的+和×和矩阵里面的运算不同,待会介绍
给定的正矩阵
过程
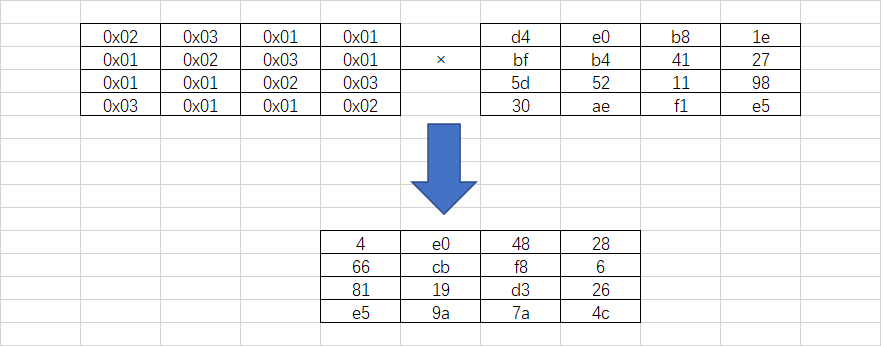
¶列混合计算
基于有限域的二维运算
¶矩阵的运算

要得到第一个数的结果,要先将第一个矩阵的第一行与第二个矩阵的第一列进行乘法,最后相加
而在列混合中,加法被替换成了异或
乘法也被修改了,注意是左移一位

这里以第一个数为例
02×d4+03×bf+01×5d+01×30,这里的+是异或
02×d4过程
00000010×11010100,因为d4首位是1,所以结果为10101000^00011011,得到10110011
同理的到第一个数为04
¶基于有限域的运算
https://blog.csdn.net/bupt073114/article/details/27382533
https://en.wikipedia.org/wiki/Finite_field_arithmetic#Multiplication
https://www.cnblogs.com/xiehongfeng100/p/4315395.html
¶有限域
有限域亦称伽罗瓦域(galois field),是仅含有限个元素的域,它是伽罗瓦(Galois,E.)于18世纪30年代研究代数方程根式求解问题时引出的,有限域的特征数必为某一素数p
¶有限域的乘法
AES的有限域是GF(2^8),也就是说从0到256都属于这个有限域内
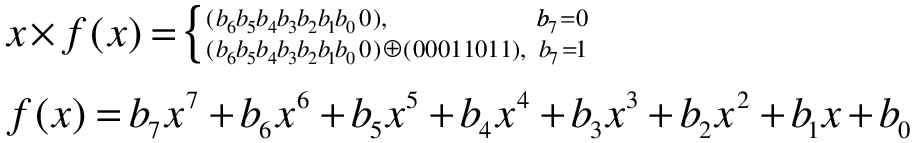
将字符转为二进制,最高位为x的7次方,最低位为x的0次方,也就是1
在AES的有限域二进制中,所有数都能通过01,02,04,08,10,20,40,80异或得到,下面是对应的二进制表示
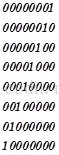
后一个分别是前一个的2倍
假设一个数a为3,那么他的二进制为00000011,也就是0x2^0x1,这里的异或在有限域中是加法
而任意一个数x和a相乘可以表示为
x×a=x×(0x2+0x1)
所以我们只需计算出
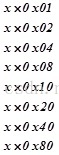
然后异或所有结果即可
¶例子
比如计算0x3a*0x24,0x3a的二进制为 00111010,
分别求,这里要注意乘二相当于左移一位,而有限域为2^8,所以可能会溢出,所以要判断最高位是否为1,如果为1的话,左移之后会溢出,就需要除以同余式,而在AES的有限域中,八次不可约同余式,这里被定义为 x8+x4+x^3+x+1,也就是异或上0x1B
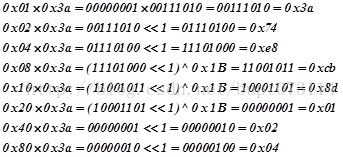
0x24=00100100,所以0x3a0x24=0x3a00100100=0x04*0x3a0x20*0x3a=0xe80x01=0xe9
代码实现
1 | unsigned char XTIME(unsigned char x) |
第一个循环实现的是计算出异或01……的值
第二个循环,逐位循环,判断是否保留该值,也就是是否要+上该值,这里的加是^
¶轮密钥加
每一列进行进行异或操作

¶密钥扩展
通过子密钥生成十轮需要的密钥
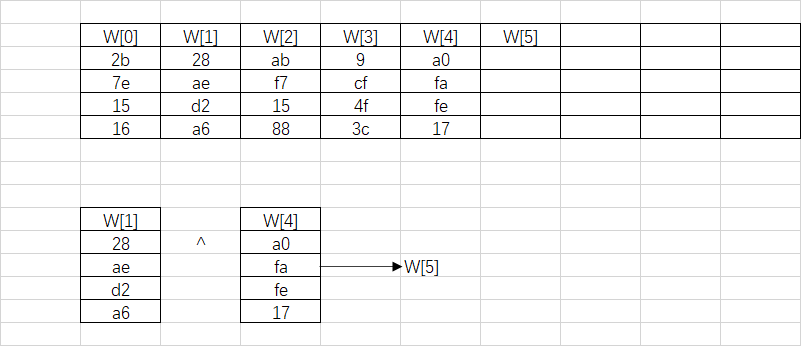
¶i不是4的倍数
第i列计算公式:
W[i]=W[i-4]^W[i-1]
¶i是4的倍数
W[i]=W[i-4]^T(W[i-1])
T函数包括三部分:字循环、字节代换、轮常量异或
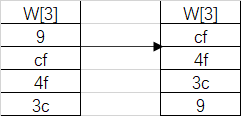
¶字循环
将一列中的四个字节循环左移一个字节,即输入[b0,b1,b2,b3]变换成[b1,b2,b3,b0],然后放在一列中
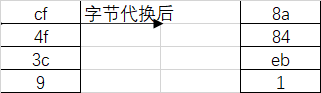
¶字节代换
对字循环的结果使用S盒进行字节代换
¶轮常量异或
将前两步的结果同轮常量Rcon[j]进行异或,其中j表示轮数。
轮常量是给定的,因为要生成十个轮密钥,所以有十个轮常量

过程
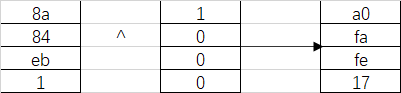
最后,将得到的结果和W[i-4]异或即可